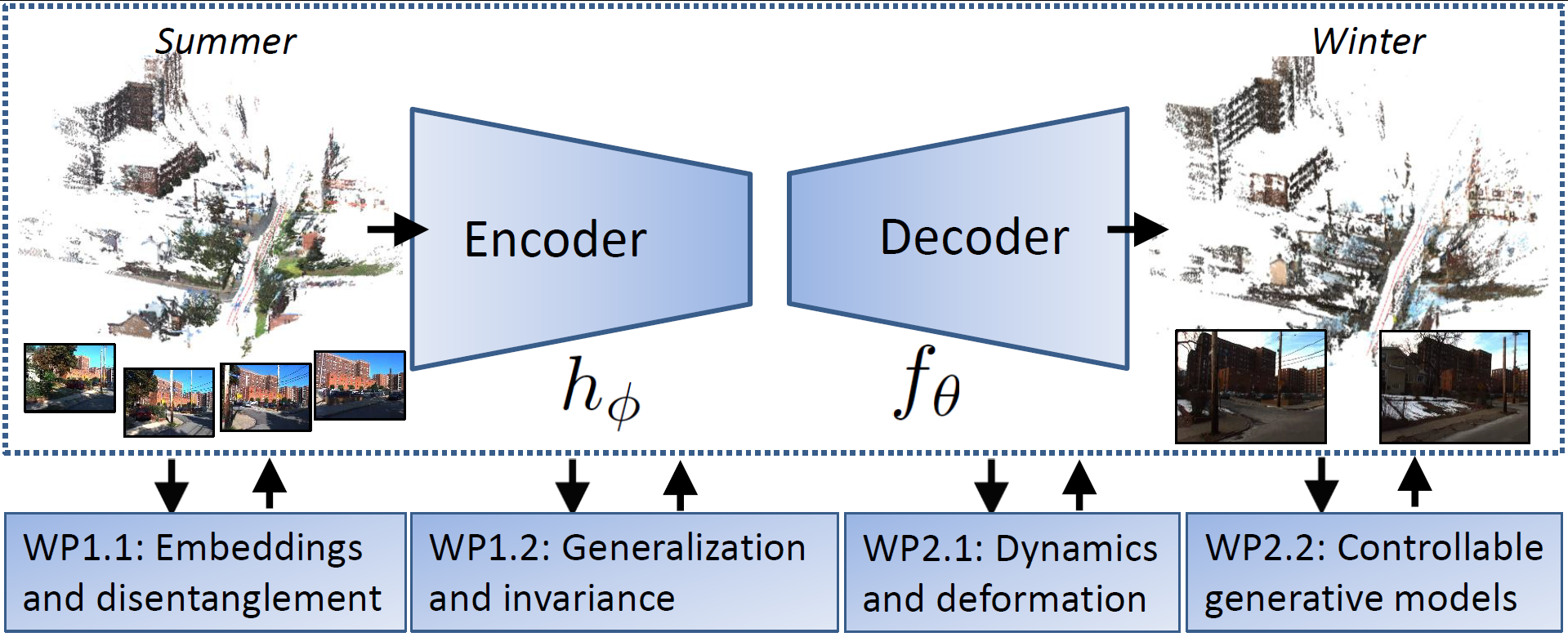
Project Parts

WP 1.1: Latent embeddings and disentanglement. Kathlén Kohn (lead), Mårten Björkman (co-lead)

Disentanglement is a widely used concept and one of the most ambitious challenges in learning. Yet, it still lacks a widely accepted formal definition. The challenge is to develop learning algorithms that disentangle the different factors of variation in the data, but what exactly that means highly depends on the application at hand. For instance, in order to be able to modify content of an indoor scene, we seek algorithms to learn situated and semantic encodings (e.g., positions and colors of objects or lighting). Several mathematical ideas have been proposed to provide a formal definition of disentanglement (e.g., statistical independence, flattening manifolds, irreducible representations of groups, direct products of group actions, but none of them applies to all practical settings where disentanglement is used. We aim to develop a more generally applicable formal definition and to study theoretical guarantees of what can be achieved with disentanglement.

Autoencoders are at the core of our project. An important aspect is their ability to memorize the training data, which has been recently explored from a dynamical systems perspective. Empirical results suggest that training examples form attractors of these autoencoders, but the theoretical reasons behind that mechanism are still not clear. Algebraic techniques can be applied in the setting of ReLU autoencoders with Euclidean loss, as the underlying geometric problem is to find a closest point on a semi-algebraic set. An open conjecture is that all training examples are attractors in a (global) minimum of the Euclidean loss of a sufficiently deep ReLU autoencoder. We aim to investigate that conjecture as well as further conditions under which attractors are formed.

WP 1.2: Generalization and invariance. Fredrik Kahl (lead)

One of the key factors for the success of deep learning for 2D image interpretation is the convolutional layer, which induces translation equivariance. That is, if the input is translated, then the output is too. It drastically reduces the number of learnable parameters, compared to a fully connected layer, and increases generalization performance. For 3D data, like point clouds, meshes and graphs, other equivariances have been investigated for classification, but except for convolutions, they are not exploited in encoder-decoder models. We will analyze, construct and develop efficient implementations for other equivariances, both for the encoder h_ϕ ◦ g(X) = g ◦ h_ϕ(X) and similarly for the decoder, f_θ ◦ g(Z) = g ◦ f_θ(Z) for all g belonging to a group. We will investigate the groups of SO(3), SE(3) and their subgroups, for instance, azimuthal rotations.

Current encoder-decoder models perform well when trained on individual categories, (e.g., “cars”), but are not able to simultaneously cope with multiple categories (e.g., “cars”, “trucks” and “buses”). By combining invariance with other generalization techniques such as multi-task learning, 3D data augmentation and self-supervision (see WP2.2), we expect to bridge the gap in building flexible generative models.

WP 2.1: Dynamics and deformation. Mårten Björkman (lead)

Earlier attempts to extend implicit neural scene representations to dynamic scenes and deformable objects, typically learn a model that controls how projection rays are bent to account for deformations observed in each input frame, with no consistency enforced over time or ability to interpolate between frames. To prevent the model from collapsing into a set of flat surfaces, some regularization of the deformation is required, which limits the amount of change that can be tolerated. We will explore methods to overcome these limitations by providing regularization in terms of trajectories modelled in a learned deformation space. We intend to learn latent space representations of deformation fields and enforce continuity by exploiting the sequential nature of the data. The ambition is to decouple deformations from geometry, aggregate information over multiple scenes, and learn deformation models that can be quickly adapted to novel scenes, by relying on meta-learning.

Deformations in the real world are typically governed by laws of physics, which can often be expressed as dynamical systems. Many deformations are cyclic in nature, such as the shape of garments on a walking person or curtains and vegetation waving in the wind. Given this observation, we aim to exploit methods such as Neural ODE to learn the dynamics of such deformations in the latent space, not just for regularization, but also to support the generation of novel trajectories.

WP 2.2: Flexible and controllable generative models. Fredrik Kahl (lead), Kathlén Kohn (co-lead)

Given a trained encoder-decoder model, we need to be able to perform inference on incomplete data. Typically, objects are only visible from a few viewpoints or even a single viewpoint, whereas the encoder-decoder model training usually relies on complete data. There are several possible approaches to cope with missing data: (i) Adapt the encoder so to accommodate missing data, (ii) Optimize the latent variable representation Z such that the it matches the given observations. More specifically, for a given 2D observation I, we add the loss function ||π ◦ f_θ(Z) − I||² and minimize over Z. We will explore both approaches, including hybrid variants depending on the application scenario.

State-of-the-art generative models like NeRF train and adapt the encoder-decoder parameters ϕ and θ using a single scene. This is not realistic when building controllable generative models. They must be able to generalize across different scenes (see WP1.2). The traditional way of training an auto-encoder is that given an input X that generates the embedding Z = h_ϕ(X), the model parameters should be chosen to match the output f_θ(Z). We will rely on two innovations to adapt to our setting. First, if the decomposable and interpretable embedding Z is modified to Z’, for instance, by changing lighting conditions, then output should be changed to X’ . More generally, given input X and modified latent embeddings Z’_i and corresponding outputs X’_i, the parameters ϕ and θ should be optimized to reproduce the original scene as well as the modified versions. Second, it will be impractical (if not impossible) to rely on 3D ground truth data for all the modified output X’_i. Instead, the typical setting is to have access to 2D observations (images) I’_i for a limited set of viewpoints and seek to minimize an objective function that incorporates losses of the type ||π_j ◦ f_θ(Z’_i) − I’_ij||² summed over all modifications i and viewpoints j. Such losses need to be combined with regularization, 3D data augmentation strategies, and efficient latent representations.